SUDOKU

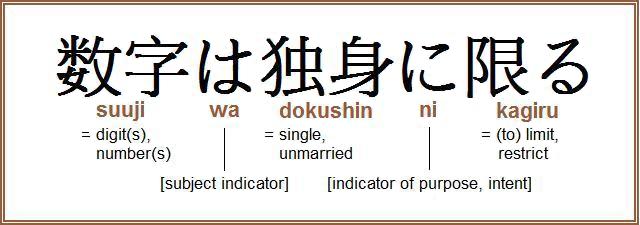
The word sudoku is the contraction of a Japanese phrase which may be translated as ‘limiting to single digits’.

A standard sudoku grid contains 81 squares formed by 9 columns and 9 rows. The whole is divided into 9 cells each of 9 squares (3x3). Three cells in line horizontally across the grid are sometimes referred to as a band, and three cells vertically as a stack.

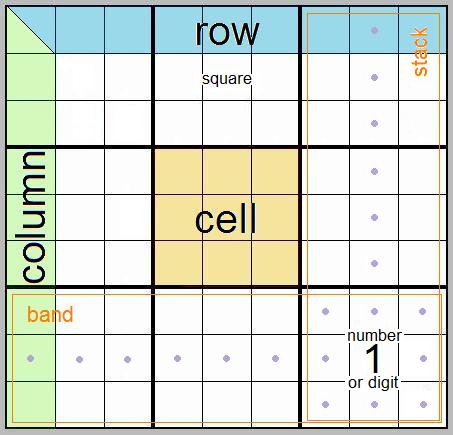
Any number, or digit, placed in a square is given the power to ‘block’ the cell and column and row that the digit inhabits. This means the same digit cannot appear again in any of those domains. In all, each digit will block 20 squares as well as filling its own square – potentially influencing about one quarter of the entire grid.

Sudoku’s challenge is to complete the puzzle grid so that every cell, column and row displays the digits 1 to 9, one appearance for each digit in whatever necessary order. A typical ‘medium’ puzzle may have about thirty digits supplied by the setter, though the number of squares filled does not necessarily determine the level of difficulty.

Solving a sudoku puzzle is a process of logic, not guesswork (which usually leads to more guesswork, and on to failure). Although the puzzle uses digits, these are merely convenient symbols and they have no numerical value as such within the grid. No mathematical knowledge is required for sudoku.

solving methods

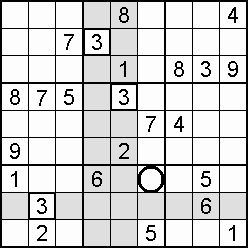
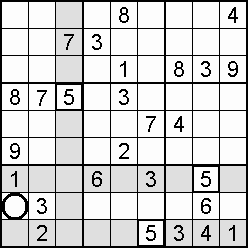
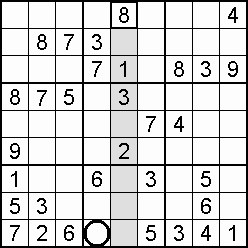
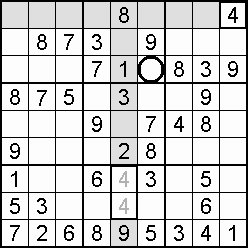
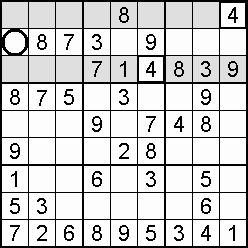
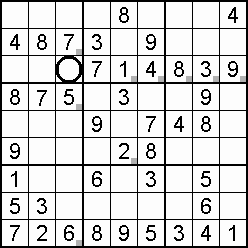
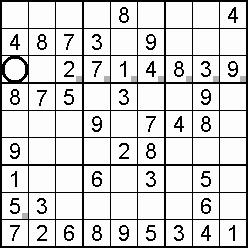
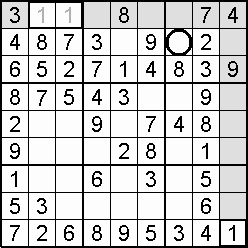
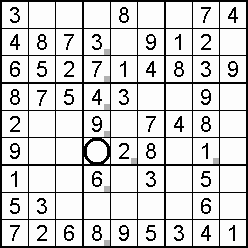
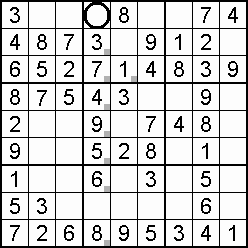
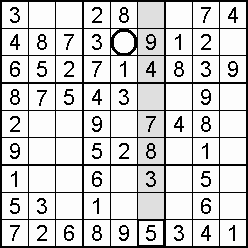
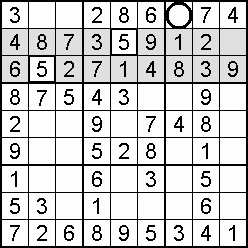
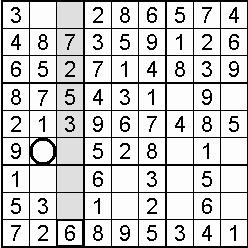
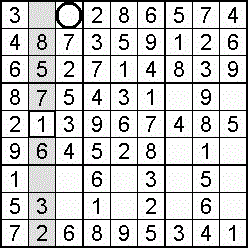
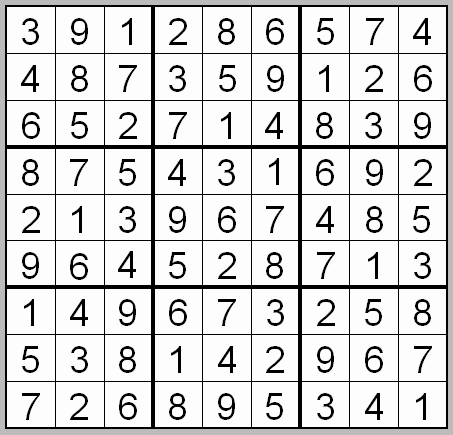
A column-and-row scan, sometimes called cross-hatching, looks for vacancies in cells by visually filling the lines (rows and columns) occupied by a particular digit. For each digit, 1 to 9 in order, the grid is swept from top left to bottom right. The method is demonstrated in the worked example that follows this section.

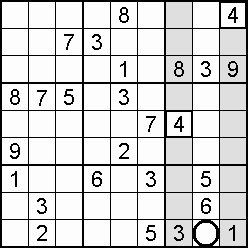
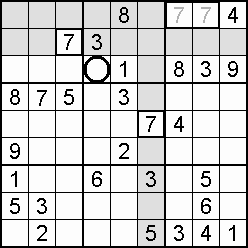
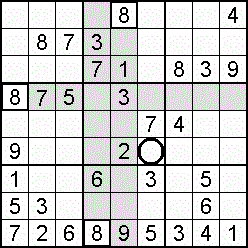
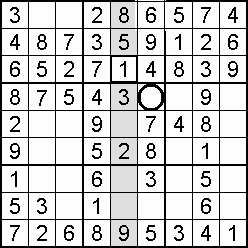
Occasionally, the column-and-row scan will stall (fail to find a vacancy), and an individual square check is the way forward. This more demanding square-to-square procedure is rewarded when eight digits are found to be blocking a particular empty square which can then be filled by the single unblocked digit. More likely to work as the grid fills.

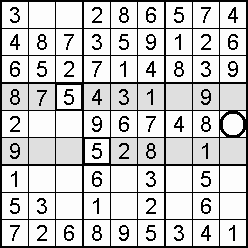
An alternative to the individual square check is to ask of domains (cells, columns, rows) where could the 1 be placed, the 2, and so on. For the most part, there will be too many squares for too many digits, but the effort may well discover that only one digit will fit a certain square. Again, a filling grid offers the better prospect of a result.

doubles and triples

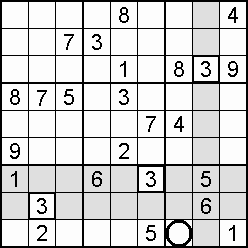
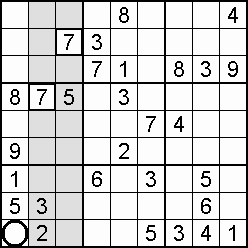
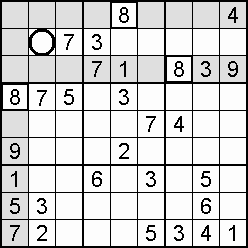
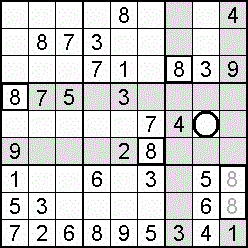
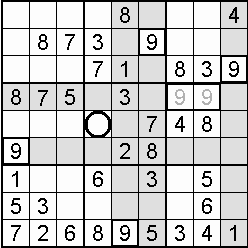
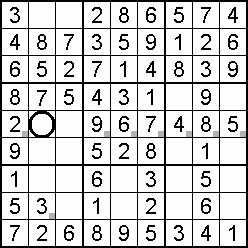
Often useful to the sudoku solving process – indeed, a lifeline in some cases – is the occurrence of a double, also called a couple, or twins. Within the one domain, two squares may be blocked to all but the same two digits. Which digit goes where is not yet decided, but the knowledge that only those squares can take only those digits means that both of the digits can be eliminated from all other squares in the domain. An example is shown in step 15 of the worked example.

Similarly, a triple (trio, threesome, triplets) may be found. If three squares within the one domain are recognised as taking only three digits (or if two of the squares will take the three digits and another square two of the digits) then the three digits can be discarded for all the other squares of the domain. The effective application of a triple is rare.

elimination

The elimination grid is designed for really stubborn puzzles. On the elimination grid, the normal square is replaced by an array containing the digits 1 to 9. By highlighting digits that are known and striking through digits that are blocked, all remaining possibilities are clearly shown. To reduce the risk of error when using the elimination grid, an alignment guide called the L-piece is recommended.

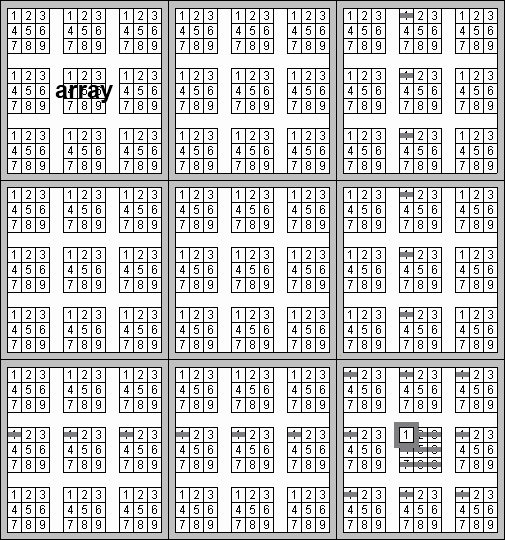
blank sudoku grid

blank elimination grid

elimination L-piece

worked example

Have a look at this step-by-step completion of a fairly difficult asymmetric puzzle. Two solving methods are used – column-and-row scan, and individual square check. A double also proves helpful.

Print puzzle on standard grid

Print puzzle on elimination grid

◀ smaller screens ▶

⟨ 1
Digits 1 and 2 offer nothing to begin with but digit 3 is well placed for blocking in the bottom band of the grid.

2 ⟩
And again.

⟨ 3
Now digit 4.

4 ⟩
So to digit 5.

⟨ 5
A 7 in the middle row of the top left cell blocks the middle row of the top right cell, leaving only the top row of that cell for its own 7 (possible squares pencilled). The blocking effect carries across to the top centre cell.

6 ⟩
Another 7, simpler.

⟨ 7
Top storey 8.

8 ⟩
A new sweep, and a 6 in the basement.

⟨ 9
Digit 8 will slot into a nearly filled bottom row. The row is finished by placing the only missing digit, 9 – two for the price of one!

10 ⟩
A further 8.

⟨ 11
Similarly to the situation in step 5, digit 8 can be pencilled in and its blocking influence used.

12 ⟩
The turn of 9.

⟨ 13
Another pencilled 9.

14 ⟩
One more.

⟨ 15
The sweep comes to a temporary halt. However, a double to the rescue. Only the digits 4 and 7 may fill two of the squares in the centre column (the tagged squares show the blocking digits).

16 ⟩
Digit 4 of the double is pencilled in to get things going again.

⟨ 17
A much easier 4.

18 ⟩
Switch to individual square checking. The tagged squares leave only the possibly for a 2 in a square in the top left cell.

⟨ 19
The same method for the same row produces a 6, which also puts a 5 in the only square left.

20 ⟩
Continuing with the method, a digit 3 is the only possibility for the top left square. A 2 completes the column.

⟨ 21
A pencilled 4 gives a result in the central cell.

22 ⟩
Combination of methods. Digit 1 must go top row of top left cell and, thanks to a placing in the central cell, digit 2 must go same row in the top centre cell. The tagged squares leave only a 7 for the top centre of the top right cell.